Graph level indices

Graph level indices

Below you will find a table to determine the foundational indices of a graph at the graph-level.

Explore the graph
Summarize the network
snafun	snafun::g_summary(x, directed = TRUE)
igraph	—
network	—
Count the number of vertices
snafun	snafun::count_vertices(x)
igraph	igraph::vcount()
network	network::network.size()
Count the number of edges
snafun	snafun::count_edges(x)
igraph	igraph::ecount(x) igraph::gsize(x)
network	network::network.edgecount(x)
Density
snafun	snafun::g_density(x, loops = FALSE)
igraph	igraph::edge_density(g)
network	# preferable for biprartite graphs network::network_density(g) # preferable for valued graphs sna::gden(g)
Reciprocity
snafun	snafun::g_reciprocity(x)
igraph	igraph::reciprocity(g)
network	sna::grecip(g,'measure = 'edgewise')
Transitivity
snafun	snafun::g_transitivity(x)
igraph	igraph::transitivity(g, type = 'global')
network	sna::gtrans(g, mode = 'digraph', measure = 'weak', use.adjacency = TRUE)
Mean distance between vertices
snafun	snafun::g_mean_distance(x)
igraph	igraph::mean_distance(g, directed = TRUE, unconnected = TRUE)
network	—
Degree distribution
snafun	snafun::g_degree_distribution(x, mode = c("out", "in", "all"), type = c("density", "count"), cumulative = FALSE, loops = FALSE, digits = 3)
igraph	igraph::degree_distribution(graph, cumulative = FALSE, mode = 'out')
network	—
Dyad census
snafun	snafun::count_dyads(x, echo = TRUE)
igraph	igraph::dyad_census(g)
network	sna::dyad.census(g)
Triad census
snafun	snafun::count_triads(x, echo = TRUE)
igraph	igraph::triad_census(g)
network	sna::triad.census(g, mode = 'digraph')
Degree assortativity
snafun	—
igraph	igraph::assortativity_degree(g, directed = TRUE)
network	—
Diameter
snafun	snafun::g_diameter(x, directed = is_directed(x), unconnected = TRUE)
igraph	igraph::diameter(g, directed = TRUE, unconnected = TRUE) # what is the vertex pair with the longest geodesic igraph::farthest_vertices(g)
network	—
Radius
snafun	snafun::g_radius(x, mode = c("all", "out", "in"))
igraph	igraph::radius(graph, mode = c("all", "out", "in", "total"))
network	—
Compactness
snafun	snafun::g_compactness(x, mode = c("out", "in", "all"))
igraph	—
network	—
Centralization
snafun	# a single function to calculate centralization (either `Freeman` or `sd`) # on a wide range of centrality indices snafun::g_centralize(x, measure = "betweenness", directed = TRUE, mode = c("all", "out", "in"), k = 3, damping = 0.85, normalized = TRUE, method = c("freeman", "sd"))
igraph1,2	# general function for Freeman centralization igraph::centralize(scores, theoretical.max = 0, normalized = TRUE) # betweenness centralization igraph::centr_betw(g, directed = TRUE) # closeness centralization igraph::centr_clo(g, mode = 'out', normalized = FALSE) # degree centralization igraph::centr_degree(g, mode = 'all') # eigenvector centralization igraph::centr_eigen(g, directed = TRUE)
network1	# general function for Freeman centralization, # include any function that calculates vertex centrality sna::centralization(g, FUN, mode = 'digraph', normalize=TRUE, ...)
Mixing matrix
snafun	snafun::make_mixingmatrix(x, attrname, by_edge = FALSE, loops = has_loops(x))
igraph	—
network	network::mixingmatrix(object, attrname, useNA = "ifany", expand.bipartite = FALSE)
Correlation between two graphs
snafun	snafun::g_correlation(g1, g2, diag = FALSE)
igraph	—
network	sna::gcor(g1, g2, mode = 'graph')
Fast-greedy community detection
snafun	snafun::extract_comm_fastgreedy(x, weights = NA, modularity = TRUE, merges = TRUE, membership = TRUE)
igraph	igraph::cluster_fast_greedy(g, merges = TRUE, modularity = TRUE, membership = TRUE, weights = NULL)
network	—
Girvan-Newman community detection
snafun	snafun::extract_comm_girvan(x, weights = NA, directed = TRUE, modularity = TRUE, edge.betweenness = FALSE, bridges = FALSE, merges = TRUE, membership = TRUE)
igraph	igraph::cluster_edge_betweenness(g, weights = NULL, directed = TRUE, edge.betweenness = TRUE, merges = TRUE, bridges = TRUE, modularity = TRUE, membership = TRUE)
network	—
Louvain community detection
snafun	snafun::extract_comm_louvain(x, weights = NA, resolution = 1)
igraph	igraph::cluster_louvain(graph, weights = NULL, resolution = 1)
network	—
Walktrap community detection
snafun	snafun::extract_comm_walktrap(x, weights = NA, steps = 4, modularity = TRUE, merges = TRUE, membership = TRUE)
igraph	igraph::cluster_walktrap(g, weights = NULL, steps = 4, merges = TRUE, modularity = TRUE, membership = TRUE)
network	—
Merge community membership
snafun	snafun::merge_membership(coms, merges)
igraph	—
network	—
1 igraph and sna only calculate `Freeman` centralization (snafun does both `Freeman` and `sd`)
2 `$res` or `$vector` return the centrality scores

Communities and other subgroups

It is informative to know that the snafun functions to extract communities yield results that can be scrutinized by igraph. The snafun package is smart enough to do this, regardless of whether the original input graph was of class igraph or network. Really handy.

Here’s an example.

# generate a random directed graph with 20 vertices and 30 edges
g <- snafun::create_random_graph(20, "gnm", m = 30)

# determine the walktrap communities
walk <- snafun::extract_comm_walktrap(g)
print(walk)
#> IGRAPH clustering walktrap, groups: 6, mod: 0.33
#> + groups:
#>   $`1`
#>   [1]  7  9 10 12 13 18
#>   
#>   $`2`
#>   [1]  5  6 16 19 20
#>   
#>   $`3`
#>   [1]  1  2 14
#>   
#>   $`4`
#>   + ... omitted several groups/vertices

# get the modularity score
igraph::modularity(walk)
#> [1] 0.3344444

# who is member of which community
igraph::communities(walk)
#> $`1`
#> [1]  7  9 10 12 13 18
#> 
#> $`2`
#> [1]  5  6 16 19 20
#> 
#> $`3`
#> [1]  1  2 14
#> 
#> $`4`
#> [1]  3 15 17
#> 
#> $`5`
#> [1]  4 11
#> 
#> $`6`
#> [1] 8

# which community is a vertex member of
igraph::membership(walk)
#>  [1] 3 3 4 5 2 2 1 6 1 1 5 1 1 3 4 2 4 1 2 2

# number of communities
length(walk)
#> [1] 6

# size of each community
igraph::sizes(walk)
#> Community sizes
#> 1 2 3 4 5 6 
#> 6 5 3 3 2 1

# which edge connects multiple communities
igraph::crossing(walk, g)
#>  [1] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [13] FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE FALSE  TRUE  TRUE
#> [25]  TRUE  TRUE  TRUE FALSE  TRUE FALSE

# plot the network, highlighting the communities
plot(walk, g)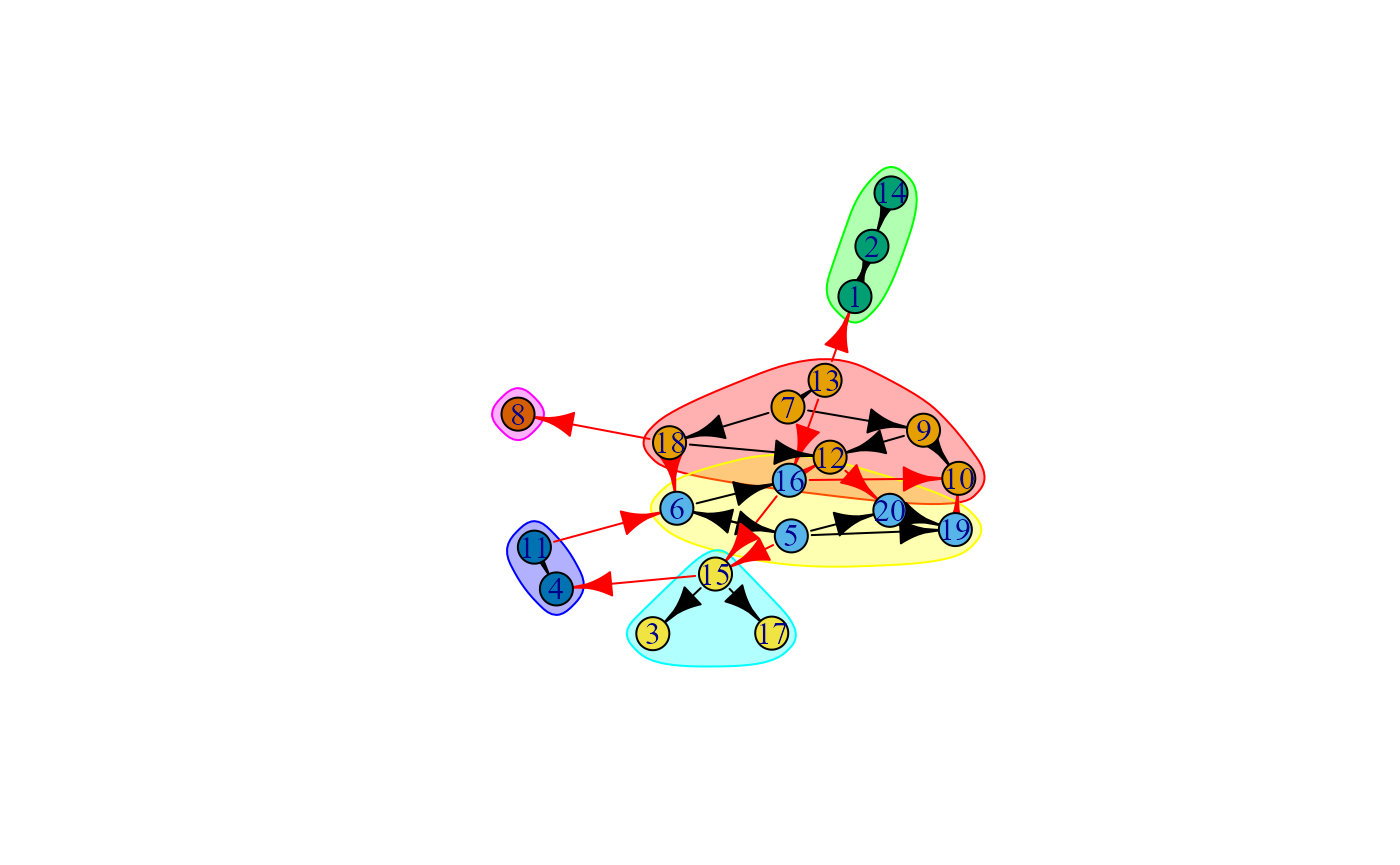

If you are so inclined, you can plot the community division as a dendrogram, as follows:

snafun::plot_comm_dendrogram(walk)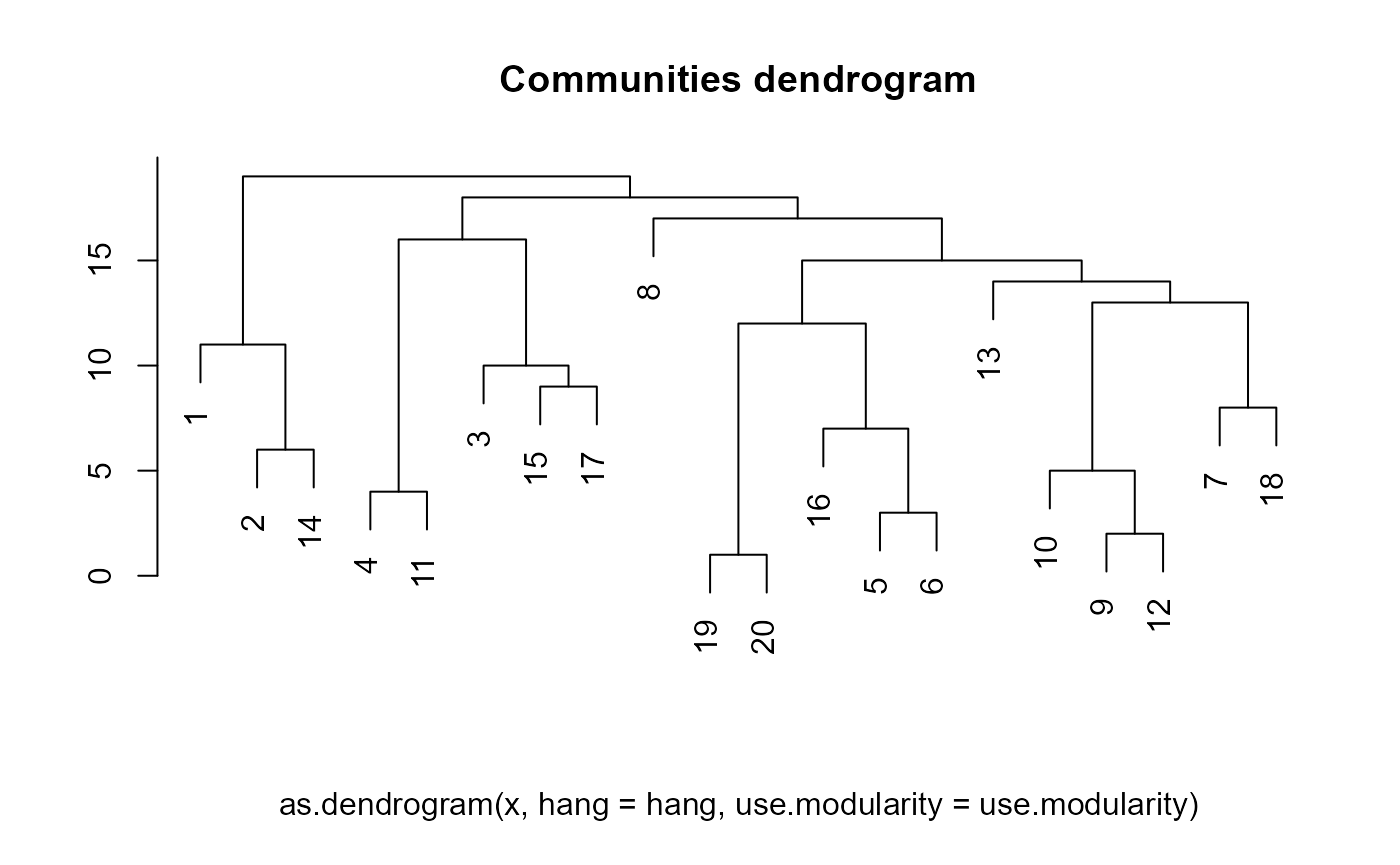

Vertex-level indices

Here are the functions to determine many of the vertex-level indices you will want to use in this course.

Explore the vertices
Degree
snafun	snafun::v_degree(x, vids = NULL, mode = c("all", "out", "in"), loops = FALSE, rescaled = FALSE)
igraph	igraph::degree(g, mode = 'out')
network	sna::degree(g, gmode = 'digraph', cmode = 'outdegree')
Betweenness
snafun	snafun::v_betweenness(x, vids = NULL, directed = TRUE, rescaled = FALSE)
igraph	igraph::betweenness(g, directed = TRUE)
network	sna::betweenness(g, gmode = 'digraph', cmode = 'directed')
Flow betweenness
snafun	—
igraph	—
network	sna::flowbet(g, gmode = 'digraph', cmode = 'rawflow')
Bonacich power centrality
snafun	—
igraph	igraph::power_centrality(g)
network	sna::bonpow(g, gmode = 'digraph')
Closeness centrality
snafun	snafun::v_closeness(x, vids = NULL, mode = c("all", "out", "in"), rescaled = FALSE)
igraph	igraph::closeness(g, mode = 'all')
network	sna::closeness(g, gmode = 'digraph', cmode = 'directed')
Harmonic centrality
snafun	snafun::v_harmonic(x, vids = NULL, mode = c("all", "out", "in"), rescaled = FALSE)
igraph	igraph::harmonic_centrality(g, vids = V(graph), mode = c("out", "in", "all"), weights = NULL)
network	—
Stress centrality
snafun	snafun::v_stress(x, vids = NULL, directed = TRUE, rescaled = FALSE)
igraph	—
network	sna::stresscent(g, gmode = 'digraph', cmode = 'directed')
Eccentricity
snafun	snafun::v_eccentricity(x, vids = NULL, mode = c("all", "out", "in"), rescaled = FALSE)
igraph	igraph::eccentricity(g, mode = 'all')
network	—
Eigenvector
snafun	snafun::v_eigenvector(x, directed = TRUE, rescaled = FALSE)
igraph	igraph::eigen_centrality(g, directed = TRUE, scale = FALSE)$vector
network	sna::evcent(g, gmode = 'digraph', rescale=FALSE)
Page rank
snafun	snafun::v_pagerank(x, vids = NULL, damping = 0.85, directed = TRUE, rescaled = FALSE)
igraph	igraph::page_rank(g, vids = V(graph), directed = TRUE, damping = 0.85, weights = NULL)
network	—
Geo k-path
snafun	# without using weights snafun::v_geokpath(x, vids = NULL, mode = c("all", "out", "in"), k = 3, rescaled = FALSE) # if weights are to be used snafun::v_geokpath_w(x, vids = NULL, mode = c("all", "out", "in"), weights = NULL, k = 3)
igraph	—
network	—
Shapley centrality
snafun	snafun::v_shapley(x, add.vertex.names = FALSE, vids = NULL, rescaled = FALSE)
igraph	—
network	—
Who are the neighbors of a vertex
snafun	snafun::extract_neighbors(x, vertex, type = c("out", "in", "all"))
igraph	igraph::neighbors(g, 'Jane', mode = 'out') # all options igraph::neighbors(graph, v, mode = c('out', 'in', 'all', 'total'))
network	network::get.neighborhood(g, 1, 'out') # all options network::get.neighborhood(x, v, type = c('out', 'in', 'combined'), na.omit = TRUE)
Neighborhood of a vertex1
snafun	—
igraph	igraph::make_ego_graph(g, order = 1, nodes = "Jane", mode = "all") # all options igraph::make_ego_graph(graph, order = 1, nodes = V(graph), mode = c("all", "out", "in"), mindist = 0)
network	sna::ego.extract(dat, ego = NULL, neighborhood = c("combined", "in", "out")) sna::neighborhood(dat, order, neighborhood.type = c("in", "out", "total"), mode = "digraph", diag = FALSE, thresh = 0, return.all = FALSE, partial = TRUE)
1 These functions serve equivalent purposes, but yield quite different kinds of outputs