Run the network autocorrelation model
Arguments
- formula
a symbolic description of the model to be fit.
- data
an optional data frame containing the variables in the model. By default the variables are taken from the environment which the function is called.
- W
Spatial weight matrix for the lagged model or the error model. This can be a matrix or a graph of class
networkorigraph.- W2
Spatial weight matrix for the error, in case of a combined model (otherwise, it is discarded). This can be a matrix or a graph of class
networkorigraph- model
character, either
lag,error, orcombined- na.action
a function (default
options("na.action")), can also bena.omitorna.excludewith consequences for residuals and fitted values - in these cases the weights list will be subsetted to removeNAsin the data. It may be necessary to setzero.policytoTRUEbecause this subsetting may create no-neighbour observations.- Durbin
default
FALSE(spatial lag model); ifTRUE, full spatial Durbin model; if a formula object, the subset of explanatory variables to lag- quiet
default
NULL, use !verbose global option value; ifFALSE, reports function values during optimization.- zero.policy
if
TRUE, the default, assign zero to the lagged value of vertices without neighbours, ifFALSEassignNA- causingspatialreg::lagsarlm()to terminate with an error- check_vars
if
TRUE, the default, a check is performed as to whether all variables on the right hand side of the formula are non-constant. Note that the function will add an intercept by default, so constants are not wanted or needed on the rhs of the formula.
Value
an object of class Sarlm
Details
This function can run the lagged network autocorrelation model, the error/disturbances model, and the combined model.
In particular, model = "lag" provides Maximum likelihood estimation
of spatial simultaneous autoregressive lag models of the form:
$$y = \rho W y + X \beta + \varepsilon$$
where \(\rho\) is found by optimize() first, and \(\beta\)
and other parameters by generalized least squares subsequently
(one-dimensional search using optim performs badly on some platforms).
With one of the sparse matrix methods, larger numbers of observations can be
handled.
When model = "error", the Maximum likelihood estimation is performed
of spatial simultaneous autoregressive error models of the form:
$$y = X \beta + u, u = \lambda W u + \varepsilon$$
where \(\lambda\) is found by optimize() first, and
\(\beta\) and other parameters by generalized least squares subsequently.
With one of the sparse matrix methods, larger numbers of observations can be
handled.
When model = "combined", Maximum likelihood estimation is performed of
spatial simultaneous autoregressive “SAC/SARAR” models of the form:
$$y = \rho W1 y + X \beta + u, u = \lambda W2 u + \varepsilon$$
where \(\rho\) and \(\lambda\) are found by nlminb
or optim() first, and \(\beta\) and other parameters by generalized
least squares subsequently.
The actual fitting of the model is performed through the lagsarlm,
errorsarlm, sacsarlm functions and the
handling of the weight matrix through the mat2listw function.
This function wraps these functions and sets some defaults that may be
useful to network analysis, but not necessarily always ideal for spatial
analysis. Also, the functions in the spatialreg package are more
flexible than was it exposed through this wrapper. So, for fitting a full
model, refer to these functions directly.
Do note, though, that those functions handle the weight matrix in a way that
is uncommon to the network analyst, and this wrapper function makes accessing
these models a lot more straightforward.
Also note that the original functions do not allow graphs of class
network or igraph to be utilized as weight matrices, which is
another benefit is our function which does make this possible.
A useful summary function is implemented within the spatialreg package.
Examples
# Simulate data for the lagged model
aantal_vars <- 10
nobs <- 50
rho = .3
coefs <- rnorm(aantal_vars)
x <- rnorm(nobs*aantal_vars, sd = 8)
x <- matrix(x, ncol = aantal_vars)
colnames(x) <- LETTERS[1:ncol(x)]
w <- sample(c(0, 1), nobs*nobs, replace = TRUE, prob = c(.8, .2))
w <- matrix(w, ncol = nobs)
diag(w) <- 0
w <- w/rowSums(w) # redundant
eps <- rnorm(nobs, sd = 5)
ie <- matrix(0, ncol = nobs, nrow = nobs)
diag(ie) <- 1
y <- solve(ie - rho*w) %*% (x %*% coefs + eps)
ix <- data.frame(y, x)
mod <- stat_nam(y ~ ., data = ix, W = w)
stat_nam_summary(mod)
#>
#> Call:spatialreg::lagsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -9.440 -3.157 0.508 2.369 10.319
#>
#> Type: lag
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -0.5578 0.9157 -0.61 0.5424
#> A -2.1712 0.0766 -28.35 < 2e-16 ***
#> B 0.9836 0.0997 9.86 < 2e-16 ***
#> C 0.2250 0.0700 3.22 0.0013 **
#> D 1.3618 0.0822 16.58 < 2e-16 ***
#> E -1.1529 0.0724 -15.93 < 2e-16 ***
#> F 0.1819 0.0908 2.00 0.0450 *
#> G 1.2718 0.0821 15.48 < 2e-16 ***
#> H 1.1002 0.0851 12.93 < 2e-16 ***
#> I 0.4845 0.0841 5.76 8.4e-09 ***
#> J 0.7199 0.1041 6.92 4.6e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.436, LR test value: 31.7, p-value: 1.77e-08
#> Asymptotic standard error: 0.0647
#> z-value: 6.74, p-value: 1.63e-11
#> Wald statistic: 45.4, p-value: 1.63e-11
#>
#> Log likelihood: -141.4428 for lag model
#> ML residual variance (sigma squared): 16.7, (sigma: 4.08)
#> Nagelkerke pseudo-R-squared: 0.98
#> Number of observations: 50
#> Number of parameters estimated: 13
#> AIC: 309, (AIC for lm: 339)
#> LM test for residual autocorrelation
#> test value: 1.2, p-value: 0.273
#>
#> Correlation of coefficients
#> sigma rho (Intercept) A B C D E F G
#> rho -0.01
#> (Intercept) 0.01 -0.68
#> A 0.00 -0.19 0.21
#> B 0.00 0.03 0.16 -0.22
#> C 0.00 0.09 -0.06 0.00 0.11
#> D 0.00 -0.26 0.10 0.06 -0.31 0.19
#> E 0.00 -0.09 -0.05 0.06 -0.32 -0.24 -0.03
#> F 0.00 0.04 -0.10 0.11 -0.16 -0.09 0.07 0.07
#> G 0.00 -0.17 0.11 0.04 0.21 0.12 -0.01 -0.10 -0.38
#> H 0.00 0.06 -0.21 0.11 -0.09 0.16 0.25 -0.02 -0.23 0.20
#> I 0.00 -0.06 0.10 0.32 -0.17 -0.30 -0.10 0.17 0.15 -0.18
#> J 0.00 -0.10 0.31 -0.12 0.30 0.24 0.09 -0.29 -0.32 0.16
#> H I
#> rho
#> (Intercept)
#> A
#> B
#> C
#> D
#> E
#> F
#> G
#> H
#> I -0.04
#> J 0.05 -0.10
#>
stat_nam_summary(mod, correlation = TRUE)
#>
#> Call:spatialreg::lagsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -9.440 -3.157 0.508 2.369 10.319
#>
#> Type: lag
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -0.5578 0.9157 -0.61 0.5424
#> A -2.1712 0.0766 -28.35 < 2e-16 ***
#> B 0.9836 0.0997 9.86 < 2e-16 ***
#> C 0.2250 0.0700 3.22 0.0013 **
#> D 1.3618 0.0822 16.58 < 2e-16 ***
#> E -1.1529 0.0724 -15.93 < 2e-16 ***
#> F 0.1819 0.0908 2.00 0.0450 *
#> G 1.2718 0.0821 15.48 < 2e-16 ***
#> H 1.1002 0.0851 12.93 < 2e-16 ***
#> I 0.4845 0.0841 5.76 8.4e-09 ***
#> J 0.7199 0.1041 6.92 4.6e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.436, LR test value: 31.7, p-value: 1.77e-08
#> Asymptotic standard error: 0.0647
#> z-value: 6.74, p-value: 1.63e-11
#> Wald statistic: 45.4, p-value: 1.63e-11
#>
#> Log likelihood: -141.4428 for lag model
#> ML residual variance (sigma squared): 16.7, (sigma: 4.08)
#> Nagelkerke pseudo-R-squared: 0.98
#> Number of observations: 50
#> Number of parameters estimated: 13
#> AIC: 309, (AIC for lm: 339)
#> LM test for residual autocorrelation
#> test value: 1.2, p-value: 0.273
#>
#> Correlation of coefficients
#> sigma rho (Intercept) A B C D E F G
#> rho -0.01
#> (Intercept) 0.01 -0.68
#> A 0.00 -0.19 0.21
#> B 0.00 0.03 0.16 -0.22
#> C 0.00 0.09 -0.06 0.00 0.11
#> D 0.00 -0.26 0.10 0.06 -0.31 0.19
#> E 0.00 -0.09 -0.05 0.06 -0.32 -0.24 -0.03
#> F 0.00 0.04 -0.10 0.11 -0.16 -0.09 0.07 0.07
#> G 0.00 -0.17 0.11 0.04 0.21 0.12 -0.01 -0.10 -0.38
#> H 0.00 0.06 -0.21 0.11 -0.09 0.16 0.25 -0.02 -0.23 0.20
#> I 0.00 -0.06 0.10 0.32 -0.17 -0.30 -0.10 0.17 0.15 -0.18
#> J 0.00 -0.10 0.31 -0.12 0.30 0.24 0.09 -0.29 -0.32 0.16
#> H I
#> rho
#> (Intercept)
#> A
#> B
#> C
#> D
#> E
#> F
#> G
#> H
#> I -0.04
#> J 0.05 -0.10
#>
plot_nam(mod)
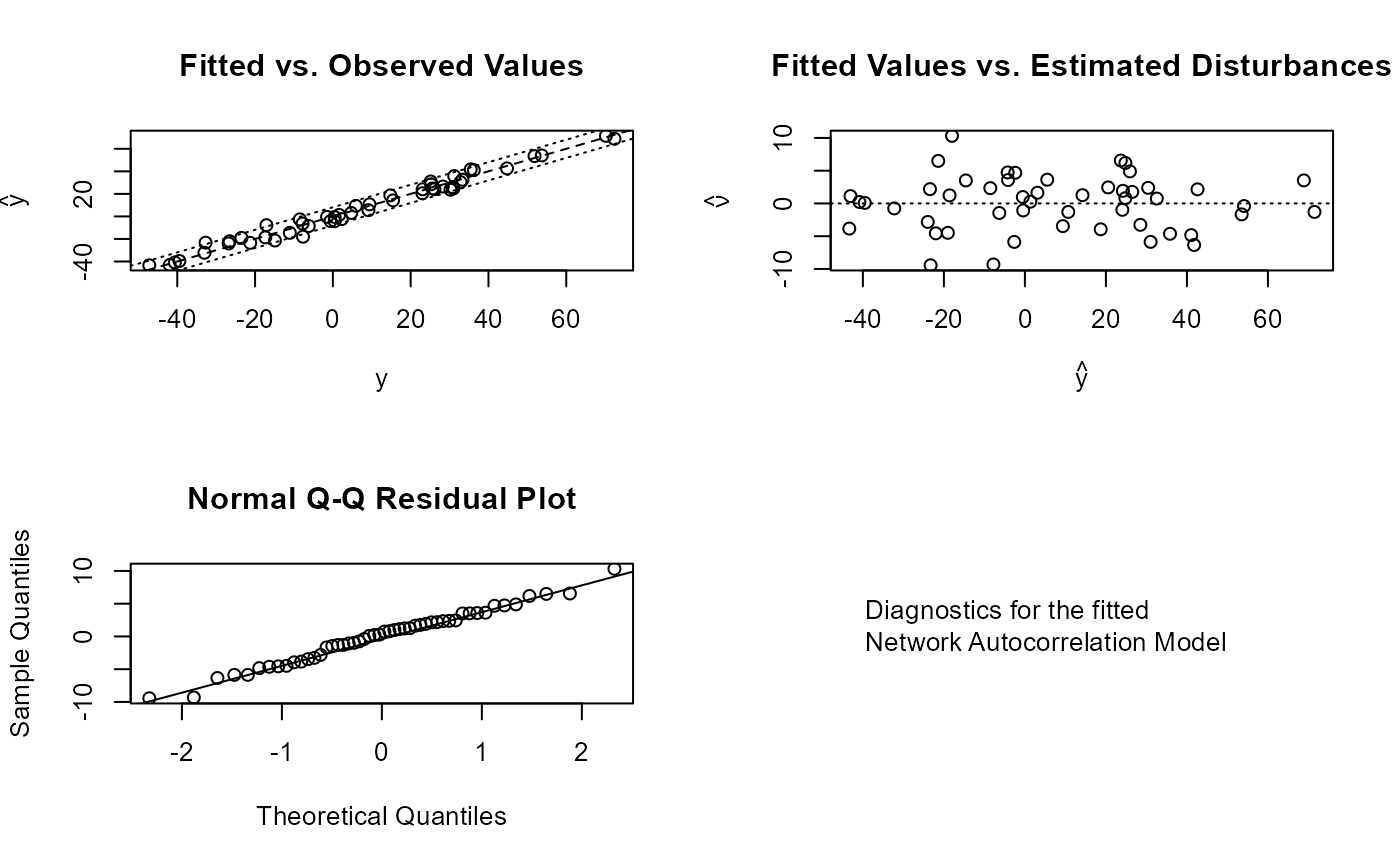 #### Now a full combined model
#Draw the AR matrix
w1 <- snafun::create_random_graph(100, strategy = "gnp", p = .2)
#Draw the MA matrix
w2 <- snafun::create_random_graph(100, strategy = "gnp", p = .2)
x <- matrix(rnorm(100*5),100,5) #Draw some covariates
r1 <- 0.2 #Set the model parameters
r2 <- 0.1
sigma <- 0.1
beta <- rnorm(6)
#Assemble y from its components:
nu <- rnorm(100, 0, sigma) #Draw the disturbances
# only for the simulation, row-standardized weights are needed
ww1 <- snafun::to_matrix(w1)
ww1 <- ww1/rowSums(ww1)
ww2 <- snafun::to_matrix(w2)
ww2 <- ww2/rowSums(ww2)
xx <- cbind(1, x)
e <- qr.solve(diag(100) - r2 * ww2, nu) #Draw the effective errors
y <- qr.solve(diag(100) - r1 * ww1, xx %*% beta + e) #Compute y
ix <- data.frame(y, x)
mod <- stat_nam(y ~ ., data = ix, W = w1, W2 = w2, model = "combined")
#> You supplied a weight matrix that was not row-normalized
#> this is still automatically done for this analysis.
#> You supplied a weight matrix (W2) that was not row-normalized
#> this is still automatically done for this analysis.
stat_nam_summary(mod)
#>
#> Call:spatialreg::sacsarlm(formula = formula, data = data, listw = W,
#> listw2 = W2, na.action = na.action, Durbin = Durbin, quiet = quiet,
#> zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.24989 -0.04861 -0.00287 0.06217 0.24593
#>
#> Type: sac
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.38425 0.07956 17.4 <2e-16 ***
#> X1 0.45165 0.01004 45.0 <2e-16 ***
#> X2 -0.01342 0.01029 -1.3 0.19
#> X3 0.93080 0.00934 99.7 <2e-16 ***
#> X4 0.74419 0.00858 86.7 <2e-16 ***
#> X5 -0.17749 0.01064 -16.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.298
#> Asymptotic standard error: 0.0396
#> z-value: 7.51, p-value: 5.8e-14
#> Lambda: 0.395
#> Asymptotic standard error: 0.322
#> z-value: 1.23, p-value: 0.219
#>
#> LR test value: 43.6, p-value: 3.46e-10
#>
#> Log likelihood: 96.6368 for sac model
#> ML residual variance (sigma squared): 0.00845, (sigma: 0.0919)
#> Nagelkerke pseudo-R-squared: 0.994
#> Number of observations: 100
#> Number of parameters estimated: 9
#> AIC: -175, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma rho lambda (Intercept) X1 X2 X3 X4
#> rho 0.00
#> lambda -0.03 -0.06
#> (Intercept) 0.00 -0.98 0.06
#> X1 0.00 -0.05 0.00 0.05
#> X2 0.00 -0.05 0.00 0.03 0.09
#> X3 0.00 0.04 0.00 -0.04 0.12 0.07
#> X4 0.00 0.09 -0.01 -0.08 -0.08 0.00 0.08
#> X5 0.00 0.21 -0.01 -0.20 -0.08 -0.11 -0.02 0.02
#>
stat_nam_summary(mod, correlation = TRUE)
#>
#> Call:spatialreg::sacsarlm(formula = formula, data = data, listw = W,
#> listw2 = W2, na.action = na.action, Durbin = Durbin, quiet = quiet,
#> zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.24989 -0.04861 -0.00287 0.06217 0.24593
#>
#> Type: sac
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.38425 0.07956 17.4 <2e-16 ***
#> X1 0.45165 0.01004 45.0 <2e-16 ***
#> X2 -0.01342 0.01029 -1.3 0.19
#> X3 0.93080 0.00934 99.7 <2e-16 ***
#> X4 0.74419 0.00858 86.7 <2e-16 ***
#> X5 -0.17749 0.01064 -16.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.298
#> Asymptotic standard error: 0.0396
#> z-value: 7.51, p-value: 5.8e-14
#> Lambda: 0.395
#> Asymptotic standard error: 0.322
#> z-value: 1.23, p-value: 0.219
#>
#> LR test value: 43.6, p-value: 3.46e-10
#>
#> Log likelihood: 96.6368 for sac model
#> ML residual variance (sigma squared): 0.00845, (sigma: 0.0919)
#> Nagelkerke pseudo-R-squared: 0.994
#> Number of observations: 100
#> Number of parameters estimated: 9
#> AIC: -175, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma rho lambda (Intercept) X1 X2 X3 X4
#> rho 0.00
#> lambda -0.03 -0.06
#> (Intercept) 0.00 -0.98 0.06
#> X1 0.00 -0.05 0.00 0.05
#> X2 0.00 -0.05 0.00 0.03 0.09
#> X3 0.00 0.04 0.00 -0.04 0.12 0.07
#> X4 0.00 0.09 -0.01 -0.08 -0.08 0.00 0.08
#> X5 0.00 0.21 -0.01 -0.20 -0.08 -0.11 -0.02 0.02
#>
plot_nam(mod)
#### Now a full combined model
#Draw the AR matrix
w1 <- snafun::create_random_graph(100, strategy = "gnp", p = .2)
#Draw the MA matrix
w2 <- snafun::create_random_graph(100, strategy = "gnp", p = .2)
x <- matrix(rnorm(100*5),100,5) #Draw some covariates
r1 <- 0.2 #Set the model parameters
r2 <- 0.1
sigma <- 0.1
beta <- rnorm(6)
#Assemble y from its components:
nu <- rnorm(100, 0, sigma) #Draw the disturbances
# only for the simulation, row-standardized weights are needed
ww1 <- snafun::to_matrix(w1)
ww1 <- ww1/rowSums(ww1)
ww2 <- snafun::to_matrix(w2)
ww2 <- ww2/rowSums(ww2)
xx <- cbind(1, x)
e <- qr.solve(diag(100) - r2 * ww2, nu) #Draw the effective errors
y <- qr.solve(diag(100) - r1 * ww1, xx %*% beta + e) #Compute y
ix <- data.frame(y, x)
mod <- stat_nam(y ~ ., data = ix, W = w1, W2 = w2, model = "combined")
#> You supplied a weight matrix that was not row-normalized
#> this is still automatically done for this analysis.
#> You supplied a weight matrix (W2) that was not row-normalized
#> this is still automatically done for this analysis.
stat_nam_summary(mod)
#>
#> Call:spatialreg::sacsarlm(formula = formula, data = data, listw = W,
#> listw2 = W2, na.action = na.action, Durbin = Durbin, quiet = quiet,
#> zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.24989 -0.04861 -0.00287 0.06217 0.24593
#>
#> Type: sac
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.38425 0.07956 17.4 <2e-16 ***
#> X1 0.45165 0.01004 45.0 <2e-16 ***
#> X2 -0.01342 0.01029 -1.3 0.19
#> X3 0.93080 0.00934 99.7 <2e-16 ***
#> X4 0.74419 0.00858 86.7 <2e-16 ***
#> X5 -0.17749 0.01064 -16.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.298
#> Asymptotic standard error: 0.0396
#> z-value: 7.51, p-value: 5.8e-14
#> Lambda: 0.395
#> Asymptotic standard error: 0.322
#> z-value: 1.23, p-value: 0.219
#>
#> LR test value: 43.6, p-value: 3.46e-10
#>
#> Log likelihood: 96.6368 for sac model
#> ML residual variance (sigma squared): 0.00845, (sigma: 0.0919)
#> Nagelkerke pseudo-R-squared: 0.994
#> Number of observations: 100
#> Number of parameters estimated: 9
#> AIC: -175, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma rho lambda (Intercept) X1 X2 X3 X4
#> rho 0.00
#> lambda -0.03 -0.06
#> (Intercept) 0.00 -0.98 0.06
#> X1 0.00 -0.05 0.00 0.05
#> X2 0.00 -0.05 0.00 0.03 0.09
#> X3 0.00 0.04 0.00 -0.04 0.12 0.07
#> X4 0.00 0.09 -0.01 -0.08 -0.08 0.00 0.08
#> X5 0.00 0.21 -0.01 -0.20 -0.08 -0.11 -0.02 0.02
#>
stat_nam_summary(mod, correlation = TRUE)
#>
#> Call:spatialreg::sacsarlm(formula = formula, data = data, listw = W,
#> listw2 = W2, na.action = na.action, Durbin = Durbin, quiet = quiet,
#> zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.24989 -0.04861 -0.00287 0.06217 0.24593
#>
#> Type: sac
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.38425 0.07956 17.4 <2e-16 ***
#> X1 0.45165 0.01004 45.0 <2e-16 ***
#> X2 -0.01342 0.01029 -1.3 0.19
#> X3 0.93080 0.00934 99.7 <2e-16 ***
#> X4 0.74419 0.00858 86.7 <2e-16 ***
#> X5 -0.17749 0.01064 -16.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Rho: 0.298
#> Asymptotic standard error: 0.0396
#> z-value: 7.51, p-value: 5.8e-14
#> Lambda: 0.395
#> Asymptotic standard error: 0.322
#> z-value: 1.23, p-value: 0.219
#>
#> LR test value: 43.6, p-value: 3.46e-10
#>
#> Log likelihood: 96.6368 for sac model
#> ML residual variance (sigma squared): 0.00845, (sigma: 0.0919)
#> Nagelkerke pseudo-R-squared: 0.994
#> Number of observations: 100
#> Number of parameters estimated: 9
#> AIC: -175, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma rho lambda (Intercept) X1 X2 X3 X4
#> rho 0.00
#> lambda -0.03 -0.06
#> (Intercept) 0.00 -0.98 0.06
#> X1 0.00 -0.05 0.00 0.05
#> X2 0.00 -0.05 0.00 0.03 0.09
#> X3 0.00 0.04 0.00 -0.04 0.12 0.07
#> X4 0.00 0.09 -0.01 -0.08 -0.08 0.00 0.08
#> X5 0.00 0.21 -0.01 -0.20 -0.08 -0.11 -0.02 0.02
#>
plot_nam(mod)
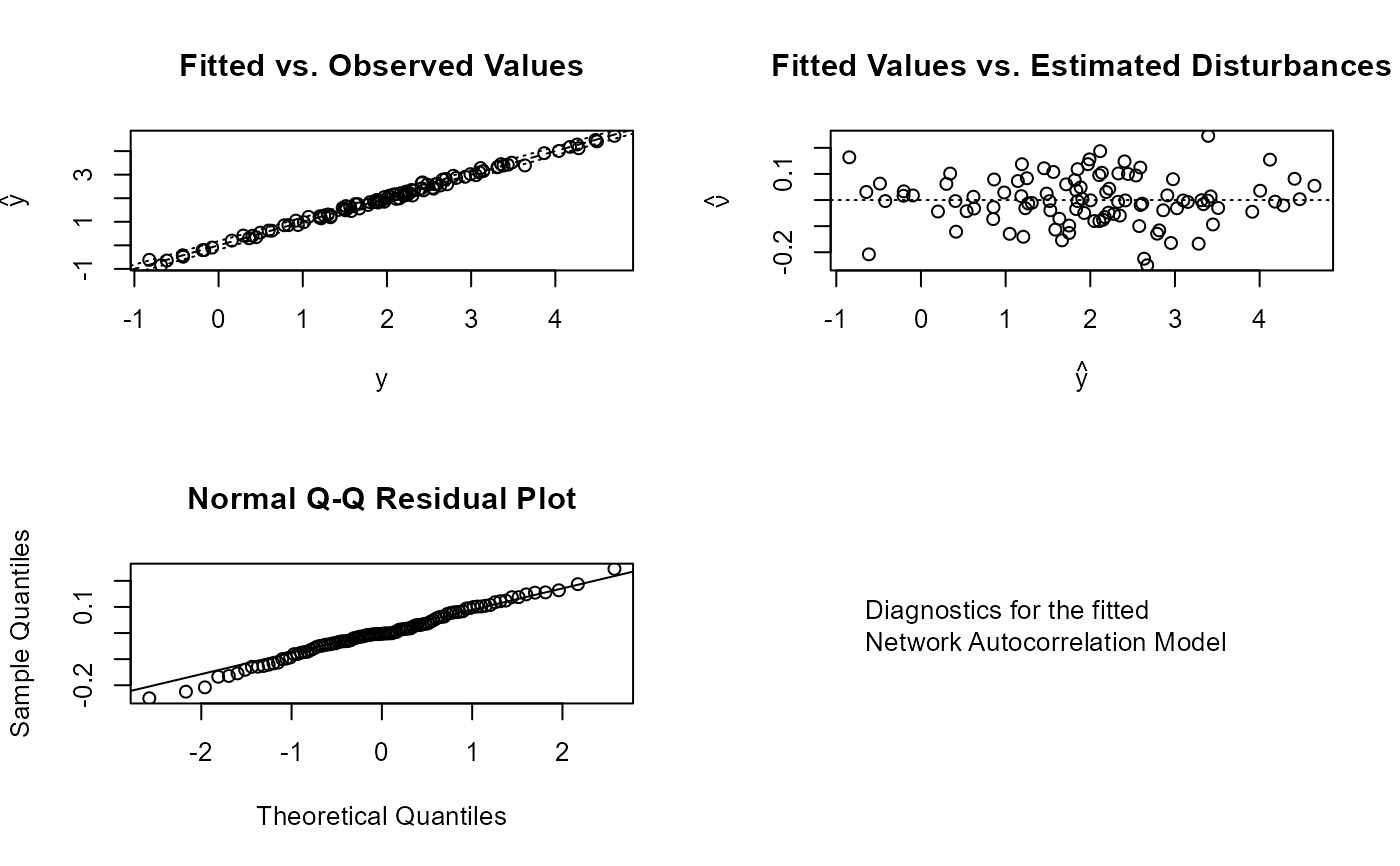 # fit the disturbances model
mod <- stat_nam(y ~ ., data = ix, W = w2, model = "error")
#> You supplied a weight matrix that was not row-normalized
#> this is still automatically done for this analysis.
stat_nam_summary(mod)
#>
#> Call:spatialreg::errorsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.3184 -0.0771 0.0101 0.0683 0.2580
#>
#> Type: error
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.96935 0.00909 216.7 <2e-16 ***
#> X1 0.45301 0.01273 35.6 <2e-16 ***
#> X2 -0.00642 0.01291 -0.5 0.62
#> X3 0.92395 0.01169 79.0 <2e-16 ***
#> X4 0.73839 0.01082 68.2 <2e-16 ***
#> X5 -0.19410 0.01325 -14.6 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Lambda: -0.272, LR test value: 0.322, p-value: 0.57
#> Asymptotic standard error: 0.427
#> z-value: -0.637, p-value: 0.524
#> Wald statistic: 0.406, p-value: 0.524
#>
#> Log likelihood: 75.01227 for error model
#> ML residual variance (sigma squared): 0.0131, (sigma: 0.114)
#> Nagelkerke pseudo-R-squared: 0.991
#> Number of observations: 100
#> Number of parameters estimated: 8
#> AIC: -134, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma lambda (Intercept) X1 X2 X3 X4
#> lambda 0.01
#> (Intercept) 0.00 0.00
#> X1 0.00 0.00 -0.03
#> X2 0.00 0.00 -0.13 0.09
#> X3 0.00 0.00 -0.04 0.13 0.08
#> X4 0.00 0.00 0.05 -0.07 0.01 0.08
#> X5 0.00 0.00 0.05 -0.09 -0.12 -0.03 -0.02
#>
stat_nam_summary(mod, correlation = TRUE)
#>
#> Call:spatialreg::errorsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.3184 -0.0771 0.0101 0.0683 0.2580
#>
#> Type: error
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.96935 0.00909 216.7 <2e-16 ***
#> X1 0.45301 0.01273 35.6 <2e-16 ***
#> X2 -0.00642 0.01291 -0.5 0.62
#> X3 0.92395 0.01169 79.0 <2e-16 ***
#> X4 0.73839 0.01082 68.2 <2e-16 ***
#> X5 -0.19410 0.01325 -14.6 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Lambda: -0.272, LR test value: 0.322, p-value: 0.57
#> Asymptotic standard error: 0.427
#> z-value: -0.637, p-value: 0.524
#> Wald statistic: 0.406, p-value: 0.524
#>
#> Log likelihood: 75.01227 for error model
#> ML residual variance (sigma squared): 0.0131, (sigma: 0.114)
#> Nagelkerke pseudo-R-squared: 0.991
#> Number of observations: 100
#> Number of parameters estimated: 8
#> AIC: -134, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma lambda (Intercept) X1 X2 X3 X4
#> lambda 0.01
#> (Intercept) 0.00 0.00
#> X1 0.00 0.00 -0.03
#> X2 0.00 0.00 -0.13 0.09
#> X3 0.00 0.00 -0.04 0.13 0.08
#> X4 0.00 0.00 0.05 -0.07 0.01 0.08
#> X5 0.00 0.00 0.05 -0.09 -0.12 -0.03 -0.02
#>
plot_nam(mod)
# fit the disturbances model
mod <- stat_nam(y ~ ., data = ix, W = w2, model = "error")
#> You supplied a weight matrix that was not row-normalized
#> this is still automatically done for this analysis.
stat_nam_summary(mod)
#>
#> Call:spatialreg::errorsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.3184 -0.0771 0.0101 0.0683 0.2580
#>
#> Type: error
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.96935 0.00909 216.7 <2e-16 ***
#> X1 0.45301 0.01273 35.6 <2e-16 ***
#> X2 -0.00642 0.01291 -0.5 0.62
#> X3 0.92395 0.01169 79.0 <2e-16 ***
#> X4 0.73839 0.01082 68.2 <2e-16 ***
#> X5 -0.19410 0.01325 -14.6 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Lambda: -0.272, LR test value: 0.322, p-value: 0.57
#> Asymptotic standard error: 0.427
#> z-value: -0.637, p-value: 0.524
#> Wald statistic: 0.406, p-value: 0.524
#>
#> Log likelihood: 75.01227 for error model
#> ML residual variance (sigma squared): 0.0131, (sigma: 0.114)
#> Nagelkerke pseudo-R-squared: 0.991
#> Number of observations: 100
#> Number of parameters estimated: 8
#> AIC: -134, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma lambda (Intercept) X1 X2 X3 X4
#> lambda 0.01
#> (Intercept) 0.00 0.00
#> X1 0.00 0.00 -0.03
#> X2 0.00 0.00 -0.13 0.09
#> X3 0.00 0.00 -0.04 0.13 0.08
#> X4 0.00 0.00 0.05 -0.07 0.01 0.08
#> X5 0.00 0.00 0.05 -0.09 -0.12 -0.03 -0.02
#>
stat_nam_summary(mod, correlation = TRUE)
#>
#> Call:spatialreg::errorsarlm(formula = formula, data = data, listw = W,
#> na.action = na.action, Durbin = Durbin, quiet = quiet, zero.policy = zero.policy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.3184 -0.0771 0.0101 0.0683 0.2580
#>
#> Type: error
#> Coefficients: (asymptotic standard errors)
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.96935 0.00909 216.7 <2e-16 ***
#> X1 0.45301 0.01273 35.6 <2e-16 ***
#> X2 -0.00642 0.01291 -0.5 0.62
#> X3 0.92395 0.01169 79.0 <2e-16 ***
#> X4 0.73839 0.01082 68.2 <2e-16 ***
#> X5 -0.19410 0.01325 -14.6 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Lambda: -0.272, LR test value: 0.322, p-value: 0.57
#> Asymptotic standard error: 0.427
#> z-value: -0.637, p-value: 0.524
#> Wald statistic: 0.406, p-value: 0.524
#>
#> Log likelihood: 75.01227 for error model
#> ML residual variance (sigma squared): 0.0131, (sigma: 0.114)
#> Nagelkerke pseudo-R-squared: 0.991
#> Number of observations: 100
#> Number of parameters estimated: 8
#> AIC: -134, (AIC for lm: -136)
#>
#> Correlation of coefficients
#> sigma lambda (Intercept) X1 X2 X3 X4
#> lambda 0.01
#> (Intercept) 0.00 0.00
#> X1 0.00 0.00 -0.03
#> X2 0.00 0.00 -0.13 0.09
#> X3 0.00 0.00 -0.04 0.13 0.08
#> X4 0.00 0.00 0.05 -0.07 0.01 0.08
#> X5 0.00 0.00 0.05 -0.09 -0.12 -0.03 -0.02
#>
plot_nam(mod)
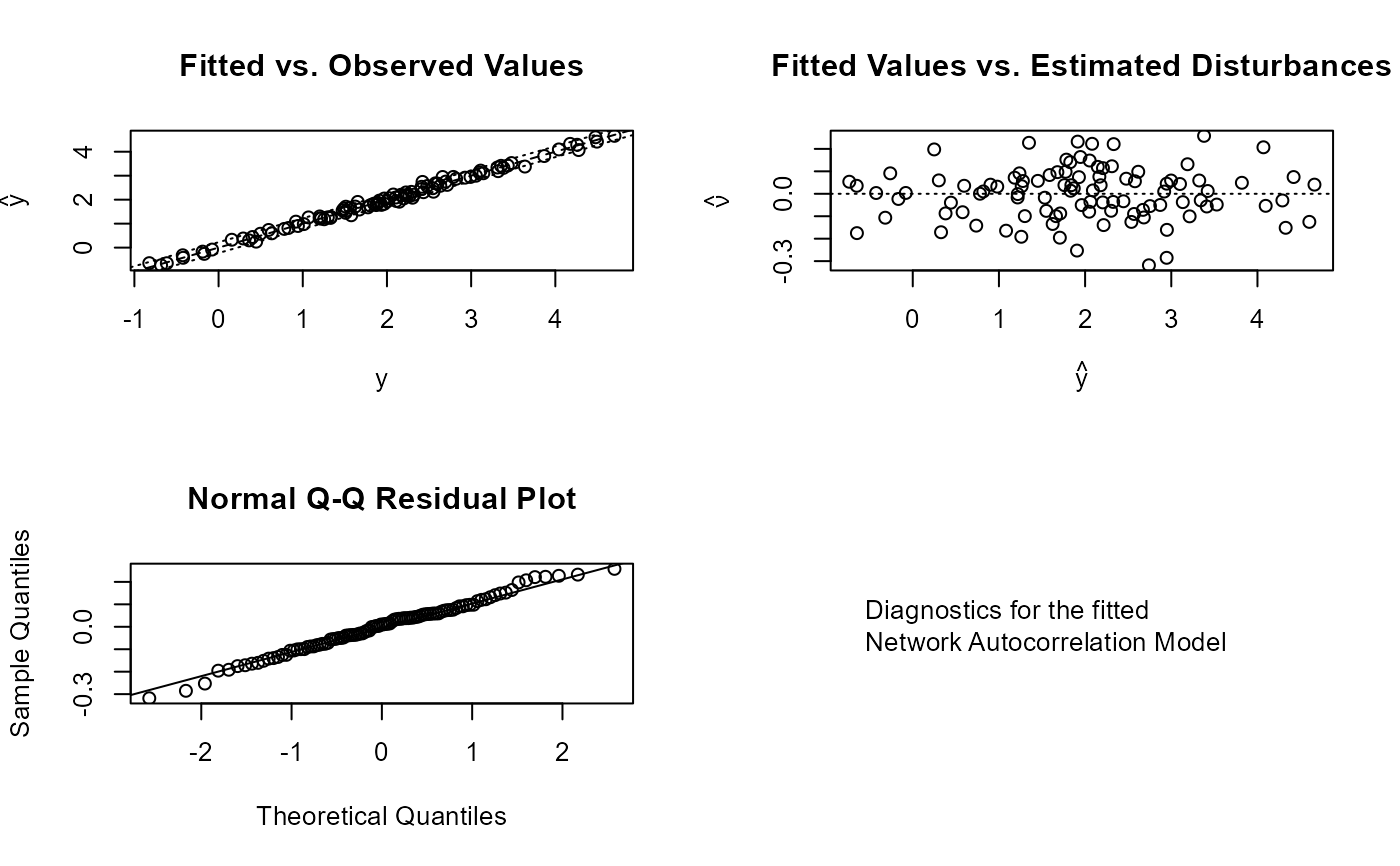 if (FALSE) { # \dontrun{
# Model from Doreian (1980)
data(huk, package = "SNA4DSData")
x <- as.matrix(cbind(Intcpt = 1, hukYX[, -1]))
lnam1 <- sna::lnam(y = hukYX$y, x = x, W1 = hukW)
lnam2 <- sna::lnam(y = hukYX$y, x = x, W2 = hukW)
lnam3 <- sna::lnam(y = hukYX$y, x = x, W = hukW, W2 = hukW)
# For comparison, the models with a row standardized W
lnam1 <- sna::lnam(y = hukYX$y, x = x, W1 = hukWstd)
lnam2 <- sna::lnam(y = hukYX$y, x = x, W2 = hukWstd)
lnam3 <- sna::lnam(y = hukYX$y, x = x, W = hukWstd, W2 = hukWstd)
# Same model with our function
nam1 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, model = "lag")
nam2 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, model = "error")
nam3 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, W2 = hukWstd, model = "combined")
} # }
if (FALSE) { # \dontrun{
# Model from Doreian (1980)
data(huk, package = "SNA4DSData")
x <- as.matrix(cbind(Intcpt = 1, hukYX[, -1]))
lnam1 <- sna::lnam(y = hukYX$y, x = x, W1 = hukW)
lnam2 <- sna::lnam(y = hukYX$y, x = x, W2 = hukW)
lnam3 <- sna::lnam(y = hukYX$y, x = x, W = hukW, W2 = hukW)
# For comparison, the models with a row standardized W
lnam1 <- sna::lnam(y = hukYX$y, x = x, W1 = hukWstd)
lnam2 <- sna::lnam(y = hukYX$y, x = x, W2 = hukWstd)
lnam3 <- sna::lnam(y = hukYX$y, x = x, W = hukWstd, W2 = hukWstd)
# Same model with our function
nam1 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, model = "lag")
nam2 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, model = "error")
nam3 <- snafun::stat_nam(y ~ ., data = hukYX, W = hukWstd, W2 = hukWstd, model = "combined")
} # }